1. CNN
이번에는 CNN 에 대해서 알아볼 차례이다. NN (Neural Network) 은 지난 시간에 Spiral data 를 Classify 하기 위해서 사용했었는데, 간단히 정리해보자면 데이터가 입력계층, 은닉계층, 출력계층을 거치며 가중치에 따라 출력이 정해지게 되는 구조이다. (각각의 Class 가 될 확률을 출력)
물론 앞서 실습해보았던 $x, y$ 좌표에 따른 Class 는 Quantitative data 였기에, 별 고민 없이 바로 입력에 $x, y$를 넣을 수 있었지만, 우리가 흔히 생각하는 이미지의 경우에는 다르다. 직관적으로 생각해 보았을 때도, 이미지는 2차원 데이터로써 존재하기에 차원이 존재하지 않는 단순 NN 에 사용하기에는 손실되는 정보 (위치와 주변 픽셀과의 조합으로써 존재하는 정보 등)가 너무나 많다. 따라서 이미지의 데이터를 손실되지 않게끔 NN 에 적용하기 위하여 CNN 이 탄생하게 되었다.
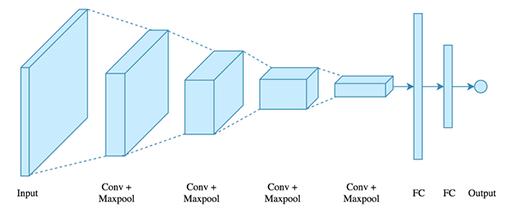
위 그림에서 보다시피, Input data 가 이미지 자체로 들어가는 것을 볼 수 있다. 하지만 layer을 거치며 점점 크기는 작아지고 두께는 두꺼워지게 되는데, 여기서 두께가 의미하는 것은 채널의 수, 즉 NN 에서의 노드 개수를 의미한다. 따라서 점점 이미지의 크기를 줄여나가는 방식으로 진행되게 된다.
자, 그렇다면 어떻게 이미지를 줄여나가는 것일까?
1) Kernel
Kernel 은 $n \times n$ 꼴의 행렬이다. 백번 입으로 설명하기보다 이미지로 보는 것이 더욱 효율적일 것 같으니 아래 그림으로 먼저 살펴보자 ㅎㅎ
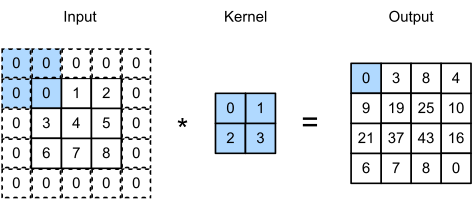
위의 그림에서 보다시피, kernel 은 input 행렬을 스캔하며 합성곱 (CNN의 풀네임은 Convolutioinal NN으로, 합성곱 신경망을 뜻한다) 을 output 으로 출력한다. 그림의 $2 \times 2$ 행렬이 $5 \times 5$ 이미지를 스캔하며 $4 \times 4$ 꼴의 행렬을 출력하는 것을 볼 수 있다. 당연하게도 kernel 의 크기가 점점 커질수록 이미지의 폭이 줄어드는 정도는 더욱 커질 것이다.
하지만, 예상했다시피 단순히 위의 방식으로만 kernel 연산을 진행한다면 수많은 layer 들을 거쳐야만 작은 크기로 줄일 수 있을 것이다. 실제로 $512 \times 512$ 정도의 이미지가 들어오게 되면, 약 500번의 kernel 들을 사용해야만 충분히 작은 크기로 이미지를 줄일 수 있을 것이다.
이에 따라 등장한 2가지 변수가 있는데, 바로 Padding 과 Stride 이다.
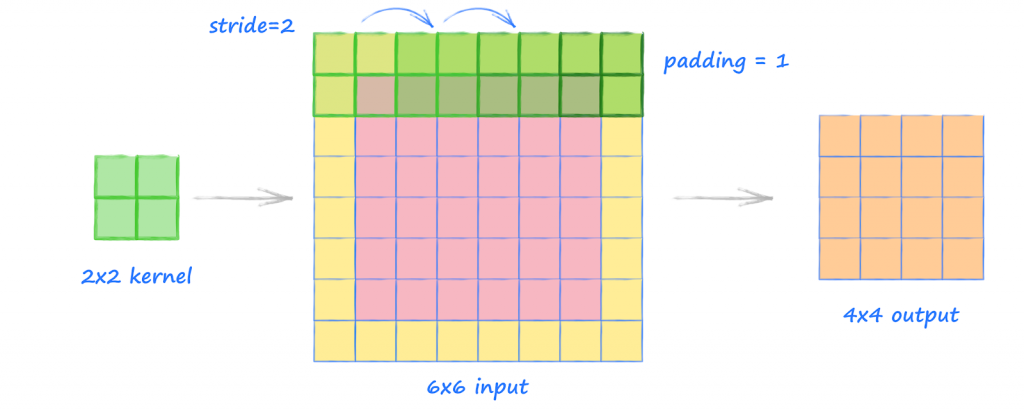
먼저, Padding 은 암호학에서도 들어볼 수 있는데, 기존의 데이터의 겉에 어떤 값들을 덧붙여 사이즈를 강제로 맞추어주는 행위이다. 위 그림에서도 볼 수 있듯이, $6 \times 6$ Input 이 들어왔음에도 불구하고, padding 을 1로 설정하여 각 변의 겉부분에 길이 1인 padding 을 진행해주었다. (우리가 입는 패딩과 비슷하죠..? ㅎㅎ)
두번째로 Stride은 직역하면 “보폭” 이라는 뜻으로, kernel 의 보폭을 의미한다. 다시 말해 몇 칸씩 건너뛰어 합성곱을 계산할 것인지를 의미한다. 위의 그림에서 보다시피 padding 이 완료된 데이터는 총 $8 \times 8$이 되는데, Stride 를 2로 설정하여 결국 $4 \times 4$ 크기의 output 이 나왔다.
이렇게 Stride, Padding, Input data의 크기에 따라 Output 의 크기가 달라지는 것을 볼 수 있는데, 추후에 코드를 짤 때는 직접 계산해야 한다. 따라서 이를 수식으로 정리해보면, 다음과 같다.
$$Width(output)= \frac{Width(input)-Size_{kernel}+2 \times Padding}{Stride}+1$$ $$Height(output)= \frac{Height(input)-Size_{kernel}+2 \times Padding}{Stride}+1$$
간단하게 $28 \times 28$ 크기의 이미지를 kernel_size = 3, stride=1, padding=1 (여기서 padding 은 output 에 적용되는 것이다) 의 변수들로 output 크기를 계산해 보았을 때, $\frac{28 – 3 + 2 \times 1}{1} + 1$ 이기 때문에 output 이 그대로 $28 \times 28$ 이 되겠다.
2) Pooling
하지만 아직 부족하다. 여전히 매우 많은 layer 들을 거쳐야 하고, 보다 효과적인 차원 감소 (Dimension Reduction) 방법이 필요하다. 여기서 나는 왜 이미지 사이즈를 줄이는 것을 “차원 감소” 라고 부르지? 라는 생각을 했었는데, 단순 이미지 크기 감소는 channel 의 수를 유지하지 못한다. 따라서 이 channel 수를 유지하며 (이는 곧 feature의 수를 줄여 Overfitting을 방지하는 효과도 있다.) 이미지 크기를 줄이는 것이 바로 Pooling 이라는 방식이다.
또한 특징 추출(Feature Extraction) 효과도 있는데, 후에 다룰 MaxPool은 각 구간에서 가장 큰 값을 채택하기에 가장 특징이 강한 부분을 추출해내어 더욱 효과적인 학습이 가능하기도 하다.
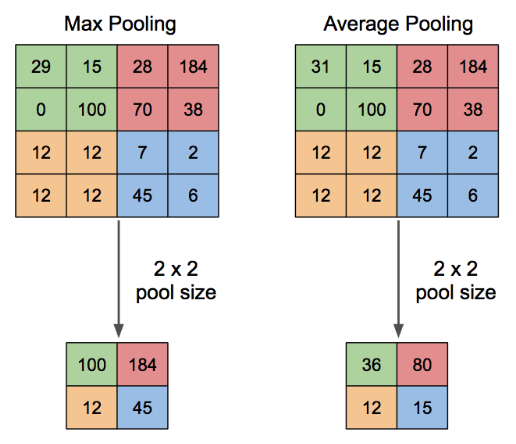
보통 Pooling 에는 크게 2가지 방식이 있는데, 앞서 말했던 Max Pooling 과 Average Pooling 이다. $n \times n$ 사이즈로 행렬을 잘라 그 구간 내에서 Max 값을 뽑거나 Average 값을 계산하여 뽑는 방식이다. (매우 간단하지만 학습의 효율과 정확도를 위해 필수적인 과정이다.)
3) ReLu
그 후에, 계속해서 Convolution 과 Pooling 작업을 반복하게 되는데, NN 이 아닌 CNN 또한 당연하게도 ReLu function 과 같은 Activation 함수가 적용되어야 한다. 비선형성을 추가하기 위하여 보통 Convolution $\rightarrow$ ReLu $\rightarrow$ Pooling 순서로 layer 을 진행해준다.
4) Full Connected Layer
이렇게 차원 축소를 진행하여 큰 $n \times n$ 크기의 이미지를 작게 만들고 나면, 결국은 Classify 를 진행해야 한다. 차원 축소가 효과적이라곤 해도, 예를 들어 $2 \times 2$ 크기만큼 줄여버리게 되면, 학습에 진행될 feature 이 매우 줄어들어 학습이 되지 않는다. 따라서 적당히 작은 크기의 행렬로 만들어 Classify 를 진행해야 한다.
그리고 CNN 은 그 Classify 방식으로 축소한 행렬을 일렬로 늘어놓아 기존의 NN 방식을 채택한다. 지금까지 이미지 자체의 정보를 유지하기 위하여 행렬로써 CNN 을 진행했었는데, 왜 갑자기 일렬로 차원을 줄여 이미지의 정보성을 삭제하느냐 물을 수 있겠지만, 사실 그 외에 Classify로 진행할 방법이 없기 때문인 것 같다. 현재 내가 블로그를 쓰는 시점에도 NN 말고 더 효과적인 방법이 존재하지 않을까 싶지만, 그 외에 Classify 를 진행할 모델이 없기에 이를 사용하는 것 같다는 생각이 든다.
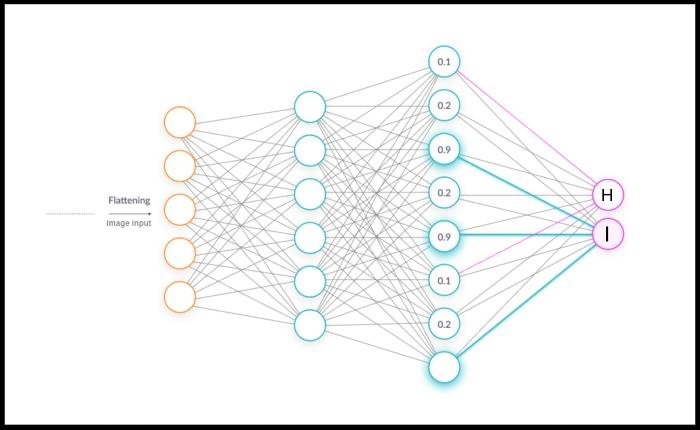
이미지를 Flattening 시켜서 이렇게 NN 모델에 넣게 되고, 이는 앞서 배웠던 Spiral data를 Classify 하는 것과 별반 다르지 않다.
2. MNIST image Classify
이제 이미지를 Classify 할 수 있는 CNN 기법에 대해 알아보았으니, 직접 MNIST의 숫자 이미지 데이터를 통해서 CNN 을 학습시켜보자.

듣기로 MNIST 는 상당히 학습에 용이한 모델을 제공하기 때문에, 최소 98% 이상의 학습 정확도를 가지고 있어야 한다고 한다.
먼저, 모델을 설계해야 하는데, MNIST 이미지 데이터를 받아왔을 때, 크기가 $28 \times 28$ 인 것을 확인할 수 있다. 따라서 다음과 같이 CNN 모델을 설계할 수 있다.
#(channel num, width, height)
(1,28,28) → {(32,28,28) → (32,14,14)} → {(64,14,14) → (64,7,7)} → (1, 3136) → (1, 1024) → (1, 128) → (1, 10)결국 마지막에 출력계층은 10가지 숫자 중 1개로 나와야 하므로 $(1, 10)$ 이 되겠고, 계속해서 Convolution 과 MaxPooling 을 이용해서 차원을 줄여나갈 수 있다.
이대로 모델을 짠다면 다음과 같은 코드가 되겠다.
class CNN(nn.Module):
def __init__(self):
super(CNN, self).__init__()
self.layer1 = nn.Sequential(
nn.Conv2d(in_channels = 1, out_channels = 32, kernel_size = 3, stride=1, padding=1, bias=True, ),
nn.ReLU(),
nn.MaxPool2d(2),
)
self.layer2 = nn.Sequential(
nn.Conv2d(in_channels = 32, out_channels = 64, kernel_size = 3, stride=1, padding=1, bias=True, ),
nn.ReLU(),
nn.MaxPool2d(2),
)
self.linear = nn.Sequential(
nn.Linear(3136, 1024),
nn.Linear(1024, 128),
nn.Linear(128, 10)
)
def forward(self, x):
x = self.layer1(x)
x = self.layer2(x)
x = x.reshape(-1, 3136)
x = self.linear(x)
# x = nn.Softmax(x)
return x주의할 부분은 forward 에 reshape 부분으로, 이미지를 Flatten 해주는 작업이다. 마지막에 Softmax 함수를 이용해서 더욱 확률을 증가시켜줄 수 있지만, 일단은 사용하지 않기로 했다.
그리고 학습은 다음과 같이 진행해줄 수 있다.
from torch.utils.data import DataLoader
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))
])
train_MNIST = torchvision.datasets.MNIST('./data', train=True, transform=transform)
test_MNIST = torchvision.datasets.MNIST('./data', train=False, transform=transform)
model = CNN()
learning_rate = 1E-3
optimizer = torch.optim.Adam(model.parameters(), lr = learning_rate)
epoch = 3
batch_size = 100
train_loader = DataLoader(train_MNIST, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(test_MNIST, shuffle=False)
# From saneo
def accuracy(predict, truth):
return torch.sum(torch.argmax(predict, axis=1)==truth)/predict.size()[0]
# train
for epoch_cnt in range(epoch):
for batch_idx, (data, answer) in enumerate(train_loader):
optimizer.zero_grad()
prediction = model(data)
loss_function = nn.CrossEntropyLoss()
loss = loss_function(prediction, answer)
loss.backward()
optimizer.step()
last_loss=loss.data
with torch.no_grad():
cnt = 0
for index, (input, output) in enumerate(test_loader):
prediction = model(input)
prediction = torch.argmax(prediction, dim=1)
cnt += torch.sum(prediction==output)
print(f"acc : {round(int(cnt)/100,2)}%, loss : {last_loss}")이미지를 텐서로 변경하고, 이를 표준화 해줌으로써 더욱 효과적인 학습을 진행할 수 있다. 또, train dataset과 test dataset 을 각각 다운받은 뒤에, 언제나 그랬든 Saneo의 accuracy 함수를 인용하여 정확도를 측정해주었다. (각각의 epoch 마다 출력했다.)
결과는 다음과 같다.

정확도가 98%로 수렴했고, Over fitting 된다면 100%가 나오는 것을 감안하면, 적절히 학습이 진행되었음을 확인해볼 수 있다 !!
