AI study – week 3 – Comibear's Blog

이번 포스팅은 ML 에 대한 다양한 개념들이 등장하기에 조금 난잡할 수도 있어 천천히 읽어주시면 감사하겠습니다..ㅎㅎ 저도 처음 공부하는지라 순서들이 뒤죽박죽일수도 있어 양해 부탁드립니다 !!

1. BGD의 한계

전 포스트에서 말했듯이, Gradient descent 에는 아래와 같이 크게 4가지 약점이 존재한다. (흔히 일반적인 GD 방식을 Batch Gradient Descent (BGD) 라고 부른다.)

과도한 연산량 & 컴퓨터 자원 소모
Local minima 현상 (지역 극솟값)
Plateau 현상 (고원 현상)
Oscillation 현상 (진동, Zigzag)

차례대로 살펴보자.

1) 과도한 연산량 & 컴퓨터 자원 소모

지금까지 경사하강법에 대한 예시를 들었던 것은 모두 변수가 1개였고, 데이터셋의 크기가 매우 작은 분석의 경우였다. 하지만 실제로 쓰이는 실제 데이터셋의 크기는 이에 비할 수 없을 뿐더러, 변수가 1000개를 넘어가는 경우 또한 존재하기에 “효율“과 “속도“를 모두 고려하여야 한다.

예를 들어 MSE의 경우를 보았을 때, 데이터셋이 $10^6$ 개만 넘어가더라도, $10^6$ 개의 제곱을 계산해야 하며, 변수가 많아질수록 차원이 늘어나 연산량이 기하급수적으로 늘 것이다.

따라서 모든 데이터셋을 한꺼번에 학습시키는 BGD의 경우에는 매우 과도한 연산량과 함께, 상당량의 컴퓨터 자원을 소모하게 되어 효율적인 측면에서 좋지 않다.

2) Local minima 현상

아마 미적분에 관해서 배웠던 분들이라면 극솟값에 대한 개념을 알고 있을 것이다. 극솟값은 한 함수의 전체적인 최솟값을 뜻하는 것이 아니라, Local 에서의 최솟값을 의미한다. 아래 그림을 살펴보면 이해가 빠를 것이다.

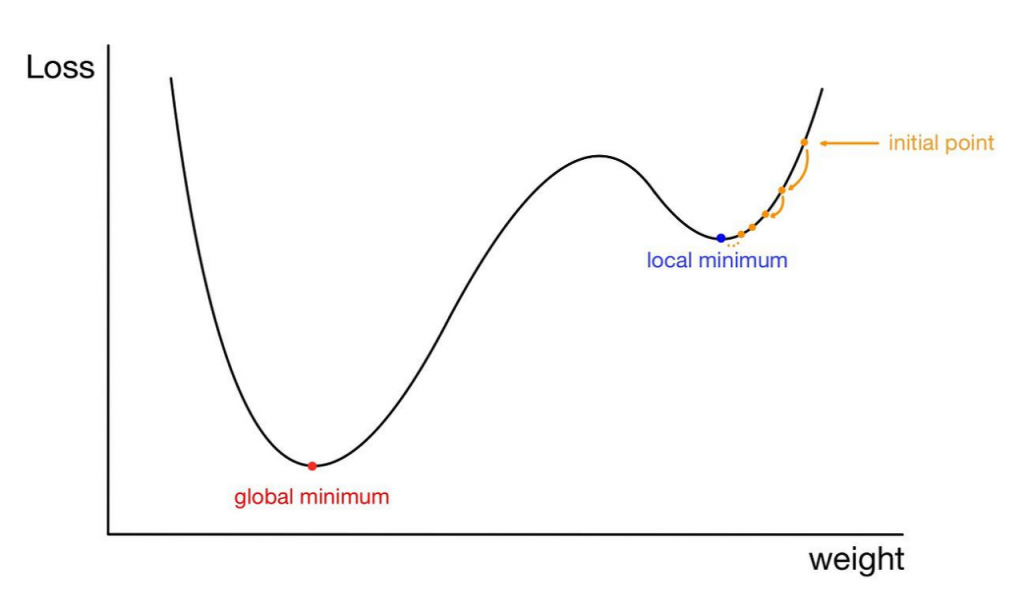
만약 경사하강법을 위의 그림과 같이 initial point 에서 진행하게 되면, 점점 local minimum 에서 수렴하는 모습을 볼 수 있는데, 실제로 $Loss$ 가 가장 작은 global minimum 과는 거리가 먼 것을 볼 수 있다. 이처럼 BGD 방식으로 학습을 시킬 때는, local minimum 에 빠질 수 있기 때문에 이를 주의해 주어야 한다.

하지만 실제로 학습을 할 때는, 가중치를 초기화하여 여러 번 학습을 시키기 때문에 local minimum 에 빠져 잘못된 학습을 하게 될 경우는 별로 없다고 한다. (하지만 주의해야 하는 한계점임은 분명하다.)

3) Plateau 현상

한마디로 고원 현상이다. 다양한 변수가 존재하는 실제 데이터셋을 이용하여 학습시켜 보면 항상 기울기가 유의미한 값으로 설정되지는 않는다. 아래 그림과 같이 매우 기울기가 작은 부분 또한 존재할 수 있다.

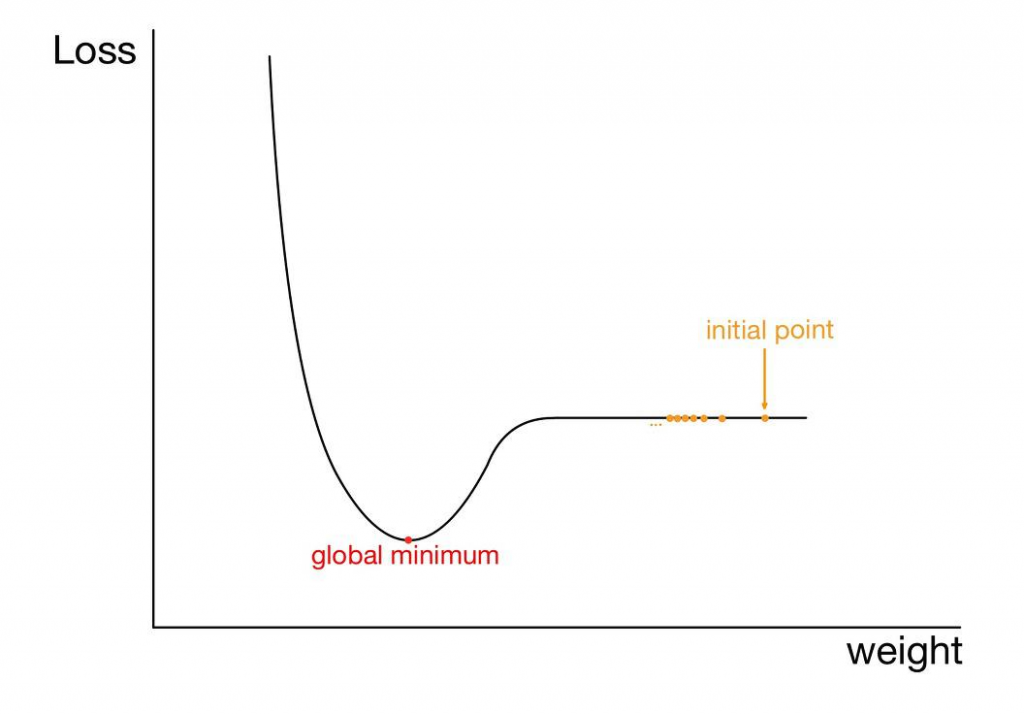
이런 경우 역시, 초기 가중치를 initial point 로 잡게 되면, 기울기가 매우 원만하기 때문에, 기울기에 비례하여 학습하는 경사하강법의 경우에는 매우 천천히 움직일 수밖에 없을 것이다. 물론 결론적으로는 최저점에 도달하겠지만, 이는 불필요하게 매우 많은 연산과 시간을 필요로 한다.

4) Oscillation 현상

이 진동 현상은 다양한 변수가 존재할 때, 특정 변수에 대해 보정이 제대로 이루어지지 않아 (보정 폭이 너무 짧아) 효율적인 측면에서 발생하는 문제이다.

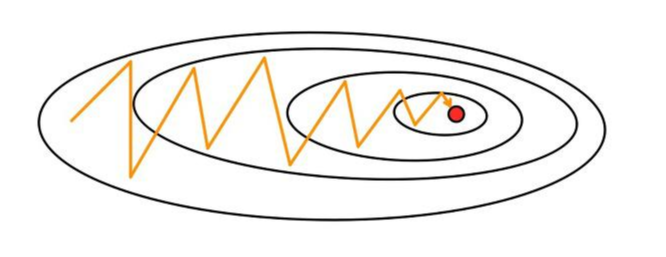
특정 가중치가 결과값에 미치는 영향이 너무 작을 경우에, 위의 그림과 같이 목표지점까지 진동하며 진행하는 형식이 나타나기도 한다. 이 또한 비효율적이기에 하나의 문제가 된다.

이런 문제들로 인하여, 더욱 효율적인 방법으로 나타난 것이 바로 SGD 방식과 MBGD 방식이다. 먼저 이런 방식들을 살펴보기 전에, 앞으로 인공지능의 “학습”시에 항상 등장하는 개념들을 먼저 배워보도록 하자.

Batch – 한번에 학습시키는 데이터셋.
Batch Size – 한번에 학습시키는 데이터셋의 크기
Epoch – 전체 데이터셋이 학습된 횟수
Iteration – 1 epoch 를 진행하는 데에 필요한 batch 의 개수

예를 들어 1000개의 데이터셋이 있다고 했을 때, 100개씩 데이터셋을 분리하게 된다면, Batch 는 총 10개 생성되며, Iteration 의 수 또한 10번이 되겠다. 그리고 당연하게도 Batch Size 는 100이다.

참고사항으로, 전체 데이터셋을 여러 개로 쪼갠다고 하여 mini-batch 라고 부르기도 한다.

2. SGD (Socastic Gradient Descent)

결국 BGD의 문제점을 보완하고, 방식을 조금 더 효율적이게 바꾼 방식이 SGD 기법이다. Socastic 의 뜻은 “확률론적” 이라는 뜻으로, BGD 처럼 전체 데이터셋을 한번에 집어넣는 것이 아닌, 1개의 단일 데이터만 뽑아 이에 대해 경사하강법을 진행하는 것이다.

당연하게도 임의의 단일 데이터를 고르기 때문에, 우리가 BGD 에서 보았던 최저점으로 직행하지는 않는다. 아래의 그림과 같이 SGD는 지그재그 모양을 그리기도 하며 “대략적인” 최저점을 향해 움직인다.

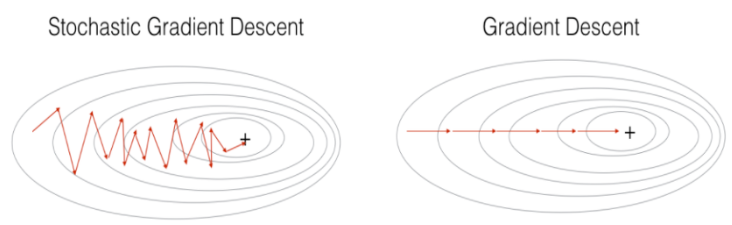
효율적인 측면에서 바라보게 되면, 1개의 데이터만 가지고 학습을 진행하기 때문에 컴퓨터가 소모하는 메모리 양이 매우 적으며, 연산 속도 또한 매우 빠르다. 물론 데이터셋이 크면 클수록 더 많은 Iteration 을 거쳐야 하지만, 이는 병렬로 계산이 되기 때문에 가속할 수 있다. 참고로 다들 AI 학습 시 GPU의 중요성에 대해 많이 들어보았을텐데, GPU 에서는 병렬 연산 가속이 되기 때문에 속도가 BGD 보다 훨씬 빠른 것을 체감할 수 있다.

추가로, BGD 에 비해 불안정한 경사하강법을 채택하기 때문에 최적의 해에 도달하기 힘들다는 단점이 존재하지만, 아이러니하게도 이런 불안정성 덕분에 Local minimum에 빠지더라도 쉽게 빠져나와 BGD 보다 Global minimum 을 찾을 가능성이 높은 장점도 있다.

3. MBGD (Mini-batch Gradient Descent)

MBGD 방식은 BGD 와 SGD 방식의 중간 지점에 있다. 말 그대로 1개만 채택하지도, 모두 채택하지도 않고 하나의 배치에서 n개만을 채택하여 이를 학습에 사용한다.

먼저 전체 데이터셋 N 개를 여러 개의 Batch 로 나누고, 이 Batch 중에서 임의의 n 개의 데이터를 택하여 학습에 사용한다. 따라서 1개만이 아닌 여러 데이터를 이용해서 학습하기에 SGD 보다는 학습 정확도가 높은 편이다. 하지만 BGD 와 SGD 의 중간에 있는 학습법임에 따라 Local minimum 문제에 걸릴 가능성 또한 높아지기도 한다.

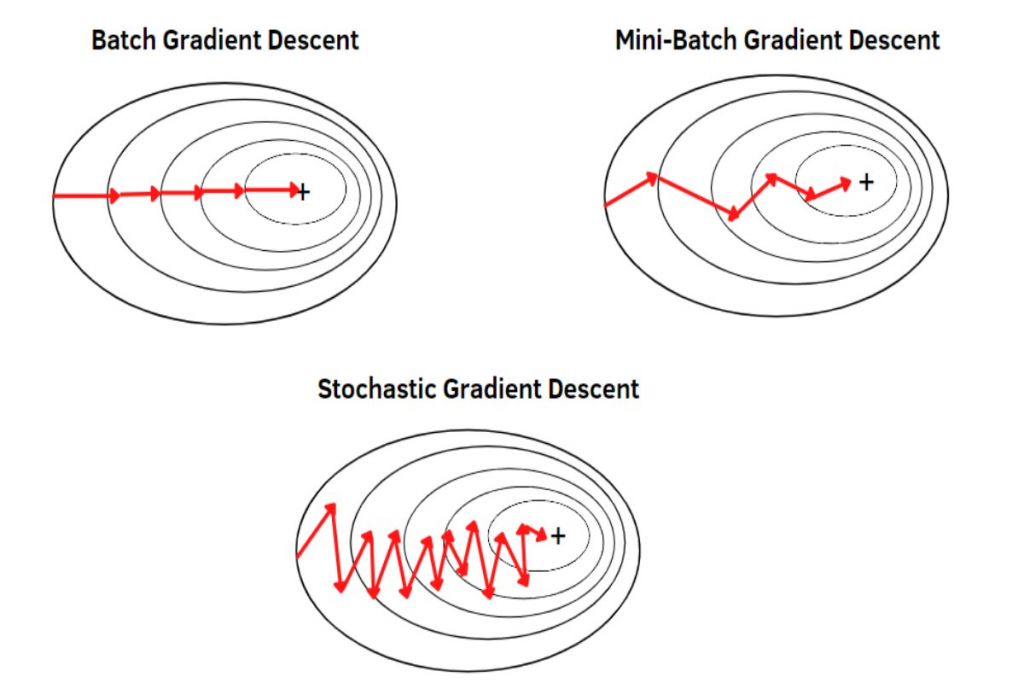
중요) 일반적으로 우리가 부르는 SGD (Socastic Gradient Descent) 는 실제론 Mini Batch Gradient Descent 를 뜻하며, 지금까지 학습했던 내용들은 기억하되, 통상적으로 말하는 SGD 는 MBGD 를 의미한다고 생각하면 되겠다.

4. NN (Neural Network)

드디어 AI 의 기초,, NN (인공신경망) 에 대해서 알아볼 차례이다. 인공신경망은 인간의 두뇌의 메커니즘에서 영감을 얻어 개발된 방식으로, 뉴런의 모습과 매우 유사하게 닮아있다.

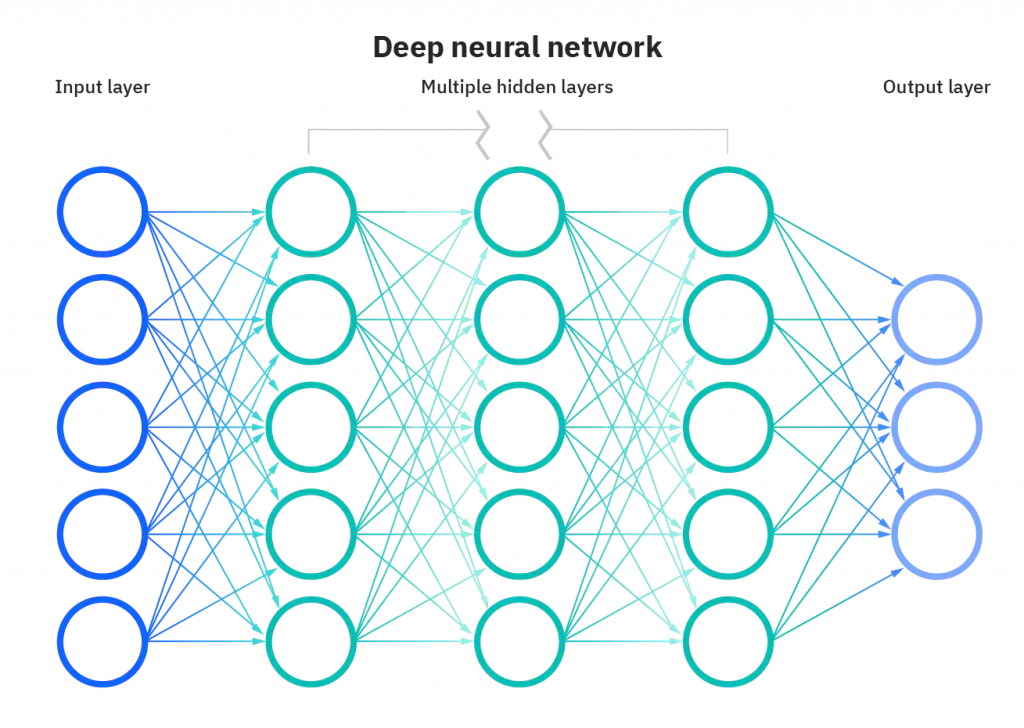
각각의 노드가 연결되어 있는 그래프 모양이라고 생각할 수 있고, dense 하게 (모든 층의 노드가 빠짐없이) 연결되어 있다. 각 노드는 하나의 선형 함수와 같다. $y = wx + b$ 꼴의 선형식을 가진 함수이며, 각각의 가중치와 편향은 하나의 가중치로 작용한다.

이런 노드들은 총 3가지 부분으로 나뉘는데, 입력 계층 (Input layer), 은닉 계층 (hidden layer), 그리고 출력 계층(Output layer)이다. 이 신경망의 목적은 여러 input 들을 넣었을 때 output 을 뽑아내는 것으로, 특히 분류 작업에 유용하다.

예를 들어 미지의 과일이 있을 때, 이 과일이 무엇인지 기계가 판단하고 싶어한다면, 출력 계층을 과일의 종류로, 입력 계층을 과일의 종류를 판단할 수 있는 요소로 넣으면 된다. 과일의 색, 맛 등을 입력 계층에 넣게 되면 이는 은닉계층을 지나며 가중치를 통해 다른 값으로 변하게 되고, 최종적으로 출력계층에 도달하게 되면 결국 어떤 과일인지에 대한 정보를 출력하는 것이다.

$$y = f(w^T x + b)$$

최종적인 하나의 노드에서의 입력과 출력에 대한 식은 위와 같다. 분명 $w$, $b$ 라는 가중치로 계산이 되어, $wx + b$의 꼴로 계산이 되는 것이라고 이해했는데, 저 $f$ 함수는 또 무엇일까..?

만약 $f$ 함수가 존재하지 않는다면, 층이 진행될수록 계속해서 $y = w^T x + b$ 가 중첩되지만, 사실은 이 식은 선형이기에 중첩되어도 선형이다. 따라서 층이 1개인 것과 다를 바가 없어지기에, 더욱 고차원적인 계산을 진행할 수 없다. 따라서 $f$ 라는 활성화 함수를 지정하여 비선형성을 추가하게 된다. (선형방정식의 결과를 활성화 함수에 다시 정의역으로 넣는다.)

5. 활성화 함수

활성화 함수는 여러 종류가 있다. 사실 여러 종류를 벗어나 비선형성을 확보하기만 한다면 뭐든지 활성화 함수가 될 수 있다. 하지만 계산의 편리성에 따라서 보편적으로 많이 사용하는 활성화 함수들이 존재한다.

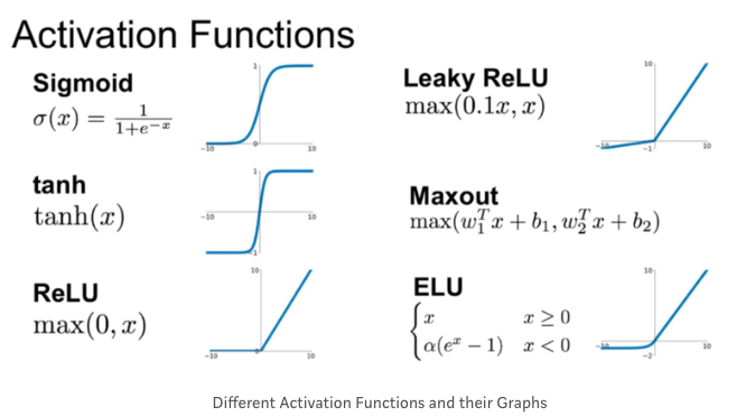
이렇게 여러 가지가 있지만, 기본적으로 알아야 하는 것은 Sigmoid, tanh, ReLu 함수 정도가 있겠다. 사실 Sigmoid 함수는 전의 포스트에서 Logistic regression 을 진행할 때 보았을 텐데, 모양은 같지만 다른 목적으로 사용된다.

1) Sigmoid

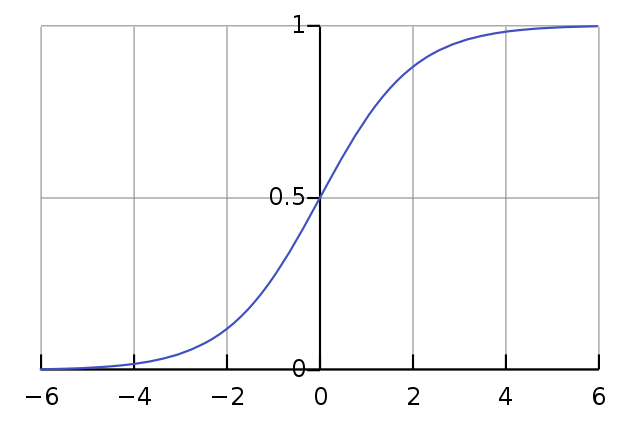
sigmoid 함수는 S 자 모양을 가지고 있는 함수이다. S 자를 45도 정도 꺾어 놓은 모양이라고 해서 이름도 Sigmoid 이다. 미분 가능성이 중요하기에 오랫동안 쓰여왔던 함수이지만, 몇 가지 단점 때문에 현재는 많이 사용하고 있지 않은 함수 중 하나이다.

1. 기울기 소멸 문제

말 그대로 기울기가 소멸하는 문제이다. Sigmoid 함수의 개형상 $|x|$ 가 커질수록 기울기가 완만해지게 된다. 그렇게 되면 추후에 역전파를 사용할 때, 기울기에 비례하여 작업하게 되어 학습이 제한되는 포화(Saturation) 상태에 이를 수 있다.

2. Non zero-centered

함수의 함숫값의 평균이 0이 아니기 때문에 ZigZag 문제가 발생하기도 한다. ZigZag 문제란 최적화를 진행할 때, 최적점까지 일직선으로 진행하는 것이 아니라, 지그재그 형태로 진행하여 비효율적으로 진행되는 문제점이다.

함숫값이 zero-centered 가 아닌 문제가 왜 ZigZag 문제로 이어지는가? 아래의 식을 보자.

$$ f = \sum{w_i x_i} + b$$ $$ \frac{df}{dw_i} = x_i$$ $$ \frac{dL}{dw_i} = \frac{dL}{df} \frac{df}{dw_i} = \frac{dL}{df} x_i$$

여기서 모든 함숫값들이 0보다 크기에 모든 $x_i$ 들이 0보다 크게 되고, $\frac{dL}{dw_i}$ 의 부호와 $\frac{dL}{df}$ 의 부호가 같게 된다. 따라서 만약 2개 이상의 변수($w_1, w_2$)가 존재하게 되면, $\frac{dL}{dw_1}$ 과 $\frac{dL}{w_2}$ 의 부호는 같게 된다.

이를 그림으로 표현해보면 다음과 같이 나타내어진다.

움직일 수 있는 방향이 제 1사분면, 제 3사분면 방향밖에 없기 때문에, 최적점까지 진행할때 위 그림과 같이 지그재그 모양으로 진행될 수밖에 없어 비효율적인 측면을 가지고 있다.

3. exp 함수로 인한 연산 속도 저하

말 그대로 exponent 로 거듭제곱 연산을 매번 해주어야 하기 때문에 연산 속도가 느리다.

2) Tanh

Sigmoid 함수와 비슷한 모양이지만, Non zero-centered 문제를 해결하기 위하여 고안된 함수이다. 모두가 알다시피, $tan$ 함수를 옆으로 세워놓은 모양이다.

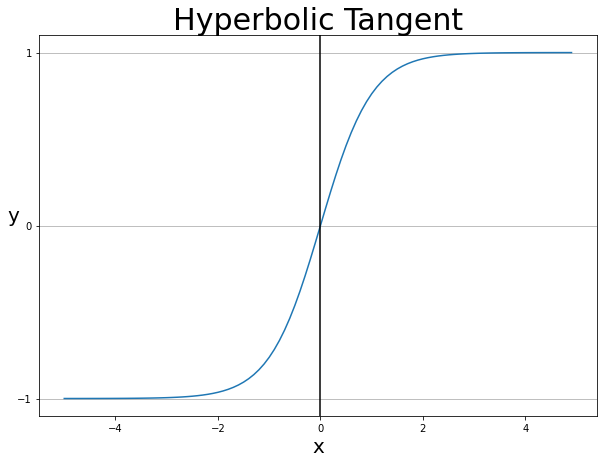
함숫값의 평균을 0으로 조정함으로써 문제를 해결했으며, 식은 sigmoid 함수를 2배하고 1을 뺀 결과이다.

$$ tanh(x) = 2\sigma{(2x)} – 1$$

하지만 여전히 기울기 소실 문제를 가지고 있어 흔히 쓰이지는 않는다.

3) ReLu

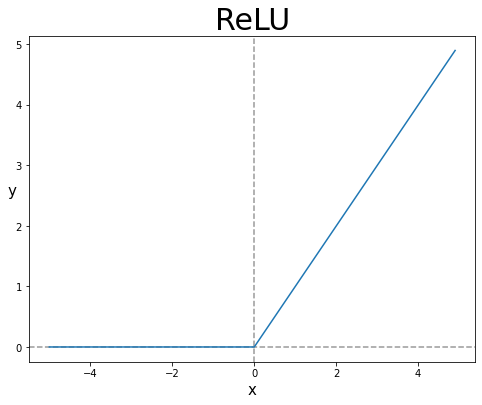
위와 같이 $x < 0$ 일때는 0, 그리고 $x > 0$ 일때는 $y = x$ 꼴의 모양을 가지고 있는 함수이다. 기울기 소실 문제가 나타나지 않는다는 장점이 있고, 함수가 직관적으로 보았을 때도 매우 매우 간단하기 때문에 연산 속도가 독보적이다. 하지만 여전히 Non zero-centered 문제 때문에 지그재그 문제가 존재하기는 하며, 이런 문제들을 해결하고자 앞서 보았던 Leaky ReLu 함수 등등 변형을 사용하기도 한다.

6. Classify

갑자기 활성화 함수를 배우다가 웬 분류?? 이라고 생각이 들 수 있겠지만, 신경망과 SGD 를 배운 시점부터는 드디어 신경망 학습을 이용해서 분류 작업을 할 수 있다 !! 👏

대표적으로 분류 문제에 등장하는 것이 나선형 데이터의 집합이다. 먼저 데이터를 살펴보자.

import torch
from toydata import ToyData

data = ToyData(num_classes=3)
x_train, y_train, x_test, y_test = data.load_data()

fig, ax = data.plot_spiraldata()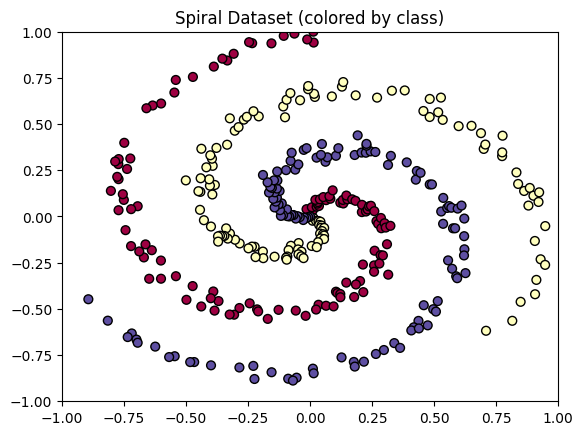

Python

(여기서 toydata.py 라는 파일로 모델을 불러왔는데, 파일이 꽤 길어 가독성에 문제가 생길 것 같아 일부러 첨부하지 않았다.. 혹시 필요한 분 계시면 댓글로 email 남겨주시면 보내드리도록 하겠습니다.)

누가 봐도 3개의 구역으로 나누어야 할 것 같은데, 이전까지 배웠던 선형 회귀나 로지스틱 회귀로는 불가능하다.. 그럼 어떻게 문제를 해결해야 할까??

바로 신경망 학습이다. 3개의 구역으로 나누기 때문에 출력 계층은 3개의 결과로 나누어지게 하고, 입력 계층은 이 그래프에서 각 점의 좌표를 넣어주면 될 것이다. 중간 은닉층은 굳이 개수를 지정할 필요는 없지만, 편의를 위해 15개로 정의하도록 하자.

import torch.nn as nn
import torch.nn.functional as F
import numpy as np

class Model(nn.Module):

    def __init__(self, num_neurons, num_classes):
        super(Model, self).__init__()
        self.linear1 = nn.Linear(2, num_neurons)
        self.linear2 = nn.Linear(num_neurons, num_classes, bias=False)

    def forward(self, x):
        x = F.relu(self.linear1(x))
        return self.linear2(x)

def accuracy(predict, truth):
    return torch.sum(torch.argmax(predict, axis=1)==truth)/predict.size()[0]

Python

torch 에서 제공하는 model 을 만들 때의 템플릿? 이 있다. 이렇게 Model(nn.Module) 을 넣게 되면 위와 같이 __init__ 함수와 forward 함수를 지정해야 한다. 이렇게 되면 자동으로 forward 함수가 __call__ 함수로 지정되기 때문에 Model() 을 함수처럼 쓸 수 있다.

그리고 accuracy라는 정확도 측정 함수를 통해서 우리의 신경망이 정확도를 높여주는지 확인해보자.

model = Model(15, 3)
learning_rate = 1E-4
optimizer = torch.optim.SGD(model.parameters(), lr = learning_rate)

Python

이렇게 정의하면, 은닉층의 노드 개수가 15개, 클래스 수가 3개인 모델이 생성되고, self.linear1 가 입력계층 – 은닉계층의 선형방정식을 담당하고, self.linear2 가 은닉계층 – 출력계층의 선형방정식을 담당하다. 따라서 forward 함수는 x 를 넣게 되면 각 선형방정식을 통과하게 되는데, 은닉계층에는 활성화 함수가 동반되어야 하기에 저런 식으로 작성해 주었다.

epoch = 15000
batch_size = 50
for epoch_cnt in range(epoch):
    idxs = np.arange(len(x_train))
    np.random.shuffle(idxs)

    for batch_cnt in range(0, len(x_train) // batch_size):
        batch_indices = idxs[batch_cnt * batch_size : (batch_cnt + 1) * batch_size]
        batch = torch.tensor(x_train[batch_indices])
        truth = torch.tensor(y_train[batch_indices])

        prediction = model(batch)
        
        loss_fn = nn.CrossEntropyLoss()
        loss = loss_fn(prediction, truth)
        loss.backward()
        optimizer.step()

        acc = float(accuracy(prediction, truth))
        print(acc)

Python

그 후에 epoch, batch size 를 지정하고, SGD 답게 위와 같이 random.shuffle 함수를 이용해서 batch 를 각 시행마다 랜덤으로 뽑아준다. 이렇게 되면 각 loss 를 CrossEntropyLoss 함수를 이용해서 계산하여 신경망이 알아서 최적화를 진행하게 된다. 그 후에 정확도를 출력해보았다.

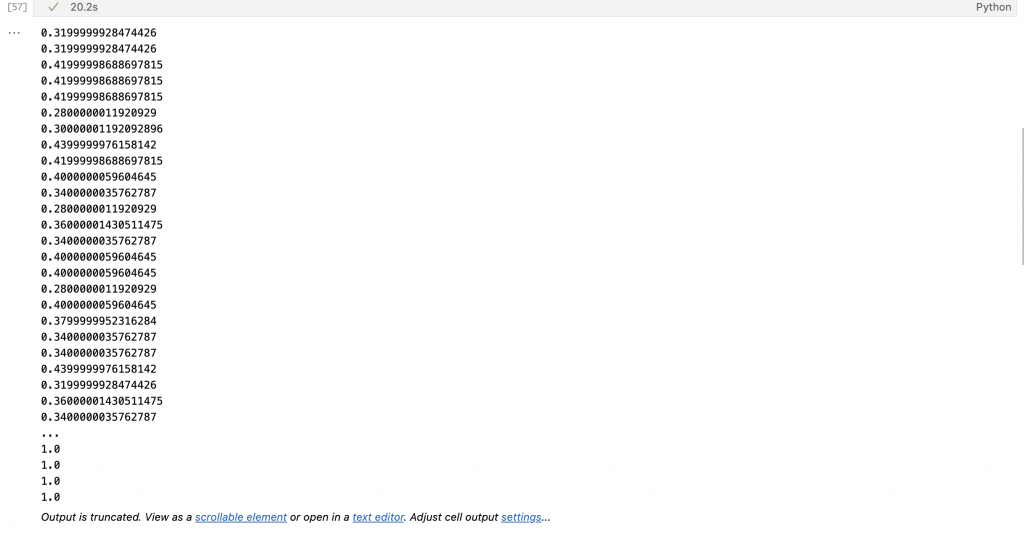
정확도가 0.3 정도부터 시작해 마지막에는 정확히 1에서 끝나는 것으로 보아, 제대로 된 최적화가 진행된 것 같다. 그럼 이제 그래프로 출력해보자.

import matplotlib.pyplot as plt
x_grid = torch.linspace(-1, 1, 100)
y_grid = torch.linspace(-1, 1, 100)

x_grid, y_grid = torch.meshgrid(x_grid, y_grid)
color = []
for i in range(len(x_grid)):
    tmp = []
    for j in range(len(y_grid)):
        pair = torch.cat((x_grid[i][j].unsqueeze(0), y_grid[i][j].unsqueeze(0)))
        output = model(pair)
        output = int(torch.argmax(output))
        tmp.append(output)
    color.append(tmp)

plt.pcolormesh(x_grid, y_grid, color, shading='auto', cmap='viridis')
plt.colorbar(label='Color')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.title('2D Plot with Color')
plt.show()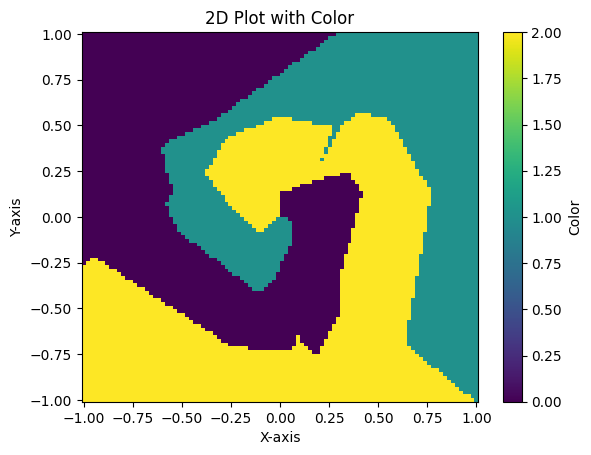

Python

그림으로 보았을 때도, 나선형으로 데이터가 거의 정확히 분리된 것을 볼 수 있다 !!