Mapping points into independent Group

Mapping is very very important method. The representative example of mapping is isogeny. Isogeny is defined with mapping function, and other many concept in math uses mapping. Rather than addressing the whole thing in this article, I plan to post with significance to come up with this mindset.

The challenge which made me think about the mapping is moduhash - [Zer0pts 2023]. Let’s see the code 🙂

moduhash – [Zer0pts 2023]

import os

flag = os.environb.get(b"FLAG", "test{dummy_dummy_dummy}")

def S(z):
	return -1/z

def T(z):
	return z + 1

def gen_random_hash(n):
	r = bytes([getrandbits(8) for _ in range(0, n)])
	return r

def to_hash(st):
	res = ""
	for s in st:
		sts = bin(s)[2:].zfill(8)
		for x in sts:
			if x == "0":
				res += "S"
			else:
				res += "T"
	return res

def hash(z, h):
	res = z
	for s in h:
		if s == "S":
			res = S(res)
		elif s == "T":
			res = T(res)
		else:
			exit()
	return res

def hash_eq(h1, h2, CC):
	for _ in range(100):
		zr = CC.random_element()
		h1zr = hash(zr, h1)
		h2zr = hash(zr, h2)
		if abs(h1zr - h2zr) > 1e-15:
			return False
	return True

CC = ComplexField(256)
for _ in range(100):
	n = randint(32, 64)
	h1 = to_hash(gen_random_hash(n))

	zi = CC.random_element()
	print(f"zi	: {zi}")
	print(f"h1(zi): {hash(zi, h1)}")

	h2 = input("your hash> ")

	if not hash_eq(h1, h2, CC):
		print("your hash is incorrect")
		exit()

print(flag)

The basic goal of this problem is to solve it by calculating a hash function consisting of a series of S and T with a pair of input and output values. The S and T functions are the following functions, which have two main characteristics.

$$S(x) = -\frac{1}{x}\,\,\,\,\,\,\;\;\;\; T(x) = x + 1$$

1. If the S function repeats, SS can be removed. (So S can be remain lonely lol)
2. Also, STSTST can be removed. (It leads to $T^{-1} = STSTS$)

Decomposition of modular group elements

The modular group $PSL_2(\mathbb{Z})$ acts on the hyperbolic half-space $H$ by
$$h\cdot z=\frac{az+b}{cz+d},\;z\in H,\;h=\begin{pmatrix}a&b\\c&d\end{pmatrix}\in PSL_2(\mathbb{Z})$$..

And, as we can easily think that the hash function can also expressed as $z=\frac{az+b}{cz+d}$. so when we calculate the value of $a, b, c, d$, maybe we could reverse it and make the hash function.

The idea to get the $a, b, c, d$ is from LLL.

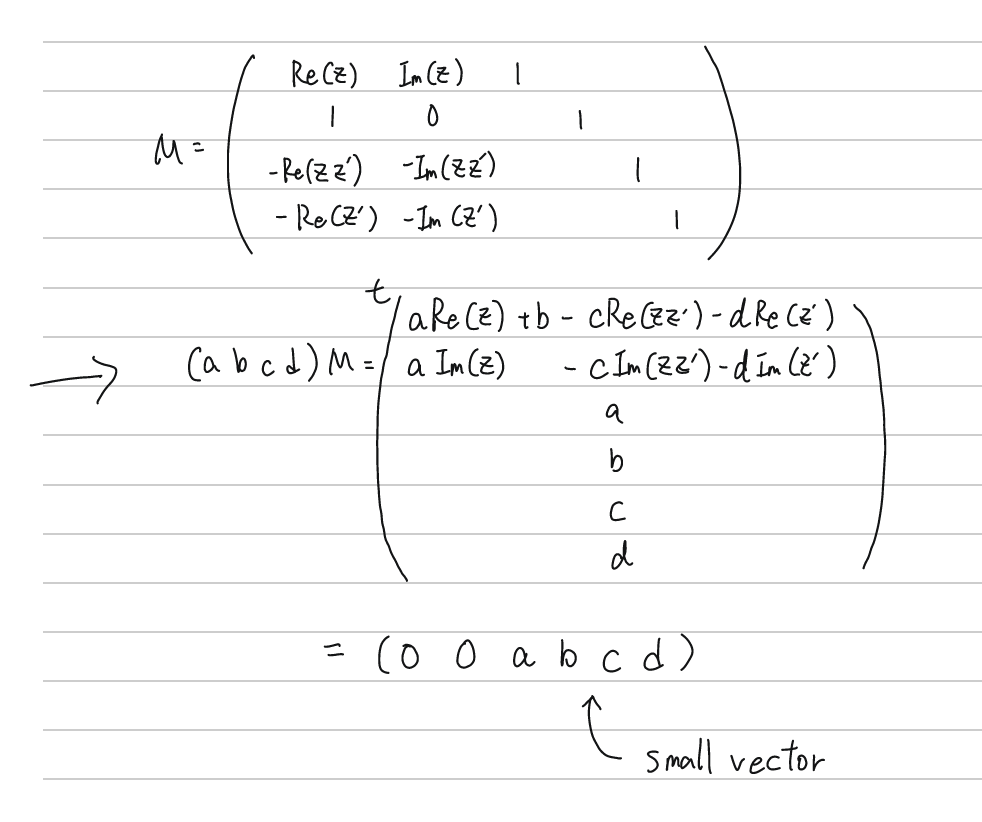
Unfortunately, however, this post will offer a different way. It is Mitsu’s official solution, and this solution is very novel and memorable.

Unlike the previous method, we will use mapping to link $Z_i$ and $h(Z_i)$ together. If we can map these two points into the independent group, and we know the mapping function, we can connect two mapping function and make whole hash function.

Then let’s define a region (set) on the complex plane that can correspond to these two given points. $ F = \left \{ point \;|\; abs(point.real()) < 0.5,\; point.norm() > 1 \right \}$

If this is represented on the coordinate plane, it is shown in the figure below.

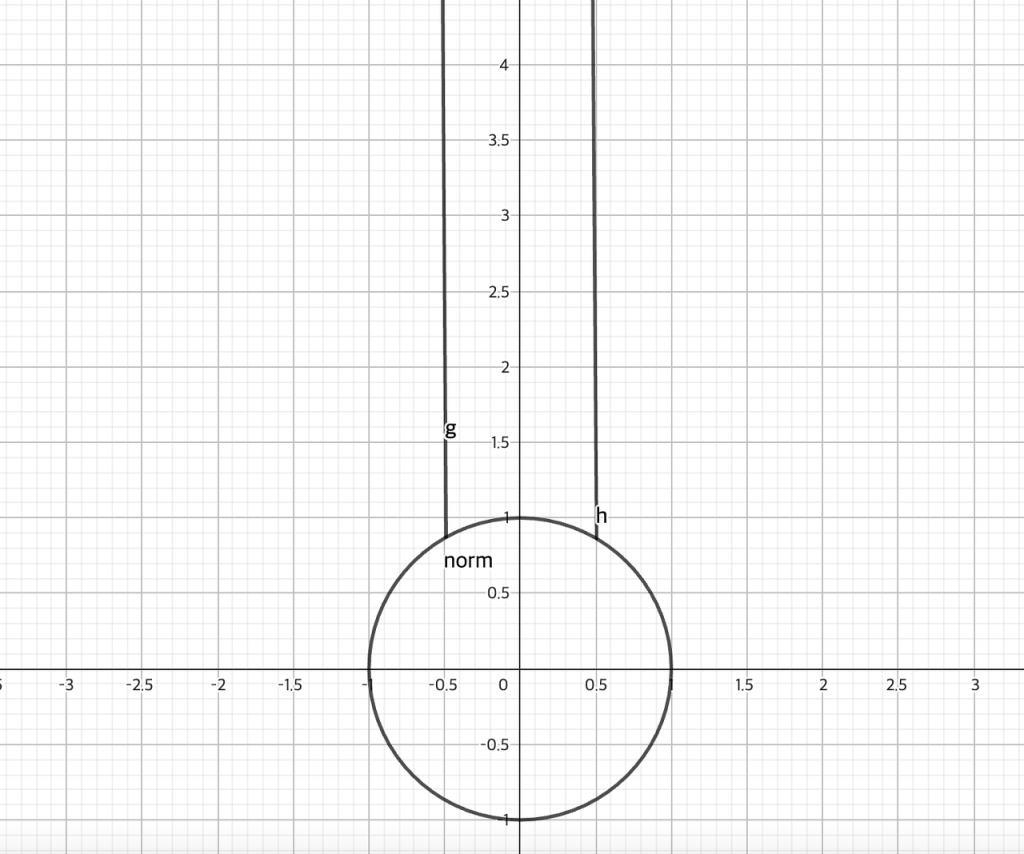
If you think about it carefully here, you can see that norm always changes based on 1 when performing an S operation. In other words, the S operation inside the circle in the picture above always goes out of the circle, and the S operation outside the circle enters the circle.

In addition, the absolute value of the real number part can be made less than 0.5 by adjusting only the integer part of all fields!!!

After all, this means that the set of $F$ mentioned above is independent of S and T operations. The points a and b on different $F$ are never connected through S and T operations.

Therefore, it may be seen that if all of the $Z_i$, $h(Z_i)$s may correspond to the $F$, it may be obvious that the same point will be made. From now on, we move the given point onto F, which is very easy, so let’s skip it.

from pwn import *
from tqdm import *

REMOTE = 1
if REMOTE:
    io = remote("crypto.2023.zer0pts.com", int(10444))
else:
    io = process(["/usr/local/bin/sage", "server.sage"])

CC = ComplexField(256)

def S(z):
	return -1/z

def T(z):
	return z + 1

def inv_T(z):
    return z - 1

def hash(z, h):
	res = z
	for s in h:
		if s == "S":
			res = S(res)
		elif s == "T":
			res = T(res)
		else:
			exit()
	return res

def hash_inv(hsh):
    payload = ""
    for h in hsh:
        if h == "S":
            payload = "S" + payload
        else:
            payload = "STSTS" + payload
    return payload

def mapping(z):
    payload = ""
    while not (z.norm() > 1 and abs(z.real()) < 0.5):
        if z.real() >= 0.5:
            z = inv_T(z)
            payload += "STSTS"
        elif z.real() < -0.5:
            z = T(z)
            payload += "T"
        else:
            z = S(z)
            payload += "S"
    payload = payload.replace("SS", "").replace("TSTSTS", "")
    return (payload, z)

for _ in trange(100):
    io.recvuntil(b"zi	: ")
    zi = CC(io.recvline().strip().decode())
    io.recvuntil(b"h1(zi): ")
    hshzi = CC(io.recvline().strip().decode())

    (map1, res1) = mapping(zi)
    (map2, res2) = mapping(hshzi)
    hsh = map1 + hash_inv(map2)

    assert abs(res1 -  res2) < 1e-15

    io.sendlineafter(b"your hash> ", hsh.encode())

flag = io.recvline().strip().decode()
print(flag)