AI study – week 1

1. Regression

AI 개념 중 가장 기본이 되는 것은 regression, 즉 회귀 분석이다. 회귀의 뜻은 “다시 돌아온다” 라는 뜻으로, 결국 평균으로 돌아옴을 의미한다. 우리가 흔히 들어봤을 선형 회귀 분석은 여러 x, y 쌍들에 대하여 가장 오차가 적은 선형 그래프를 찾아내는 분석법이며, 결국 이는 후에 x값이 주어졌을 때, y의 대략적인 값을 예측할 수 있게 한다.

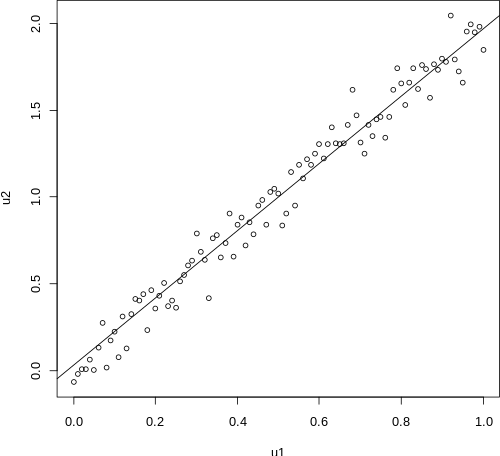
이 회귀 분석은 크게 2가지 회귀 분석으로 나뉘어진다.

1. Linear regression (선형 회귀 분석)
2. Logistic regression (로지스틱 회귀 분석)

이 둘은 모두 어떤 한 “그래프” 를 이용해서 규칙성을 찾아내는 분석법이지만 Linear 방식은 연속적인 값을 목표로 하며, Logistic 방식은 불연속적인, 즉 구간을 나누어 이산적인 데이터로 구분하기 위한 분석법이다. 그래서 Logistic regression은 일종의 classify 방식으로 생각할 수도 있다.

2. Linear regression

선형 회귀 모델의 식은 다음과 같다.

$$F(m,b;x)=mx+b$$

앞으로 많이 보게 될 수식 표현법인데, $F$ 라는 함수에서 세미콜론을 기준으로 왼쪽에 있는 변수들은 추후에 $x$와 $y$값을 기반으로 정해질 가중치(?) 라고 생각할 수 있고, 오른쪽은 독립변인(input)이 된다.

결국 $N$ 개의 $x, y$ 쌍들을 통해서 $m,b$ 값을 정의할 수 있고, 이렇게 정해진 변수들로 이루어진 그래프는 곧 주어진 쌍들에 가장 적합한 선형 회귀 그래프가 되는 것이다.

그렇다면 자연스럽게 우리는 한가지 질문이 떠오를 것이다. 어떻게 $m$, $b$라는 변수를 정의할 것인가?

– 최소제곱법 –

직관적으로 보았을 때, 우리는 오차를 최소로 하기 위해서 모든 오차의 합이 가장 작도록 만들어야 한다. 그렇기에 모든 오차들을 더했을 때 가장 작은 오차값을 가지는 선형식을 찾기를 목표로 하지만, 오차값은 항상 양수가 되지는 않는다는 문제점이 존재한다.

여러 쌍들의 데이터가 존재할 때, 임의의 식을 잡을 때 오차가 양수가 되는 경우와 음수가 되는 경우가 모두 존재하기 때문에 오차값이 실제로 큰 값을 가지더라도 실제로 더했을 경우 값이 매우 작아지는 경우가 생길 수 있다.

이런 오차의 크기를 고려해줄 수 있는 방법은 대표적으로 2가지가 있는데, 바로 절댓값과 제곱이 있다. 두 방식 중에서 더 정확하고 간단하게 선형식을 도출할 수 있는 것은 절댓값이 맞지만, 우리의 목표는 “오차의 최솟값”을 구하는 것이다. 물론 간단한 단순회귀분석 (변수가 하나인) 의 경우에는 쉽게 계산이 가능하겠지만, 문제가 더욱 복잡해질수록 우리는 “미분가능성” 을 고려해야 한다. 절댓값은 미분이 불가한 구간도 생기게 되어 제곱의 합을 더하는 방식이 더욱 효과적으로 작용하게 된다.

따라서 최소제곱법의 식을 다음과 같이 나타낼 수 있다.

$$\mathcal{L}(m,b;(x_n,y_n^{true})^{N-1}_{n=0})=\sum^{N-1}_{n=0}(y^{true}_n-F(m,b;x_n))^2$$

$\mathcal{L}$이라는 값은 Loss의 약자로, 오차의 크기를 나타낸다. 그리고 true 라는 태그는 실제 값, 즉 여러 $x, y$ 쌍에서 실제로 가지고 있는 $y$의 값을 의미한다. (추후에 선형방정식을 이용하여 각 $x$ 당 $y$의 값을 예측할 것이기에 true라는 태그로 “실제” 와 “예측” 을 구분해준다.)

결국 Loss의 값이 가장 적은 $m, b$의 값을 찾아야 하고, 이는 편미분을 이용하여 쉽게 구해줄 수 있다.

$$\frac{\partial\mathcal{L}(m,b)}{\partial m} = \sum^{N-1}_{n=0}(2x^2_nm+2bx_n-2y_n^tx_n)$$

$$\frac{\partial\mathcal{L}(m,b)}{\partial b} = \sum^{N-1}_{n = 0}(2b + 2mx_n – 2y_n^{true})$$

따라서 이 두 식을 연립해보면 다음과 같이 $m, b$ 값이 도출되게 된다.

$$m^* = \frac{\sum{x_n y_n} – \frac{1}{N} \sum{x_n}\sum{y_n}}{\sum{x_n^2} – \frac{1}{N}(\sum{x_n})^2}, \;\;b^* = \overline{y} – m^* \overline{x}$$

살짝 분산 & 표준편차 vibe…

– 경사하강법 –

앞선 최소제곱법을 이용해서 우리는 선형 회귀식을 계산할 수 있었다. 하지만 모든 회귀가 이렇게 간단한 식으로, 그리고 2~3차원으로 나타내어지지 않는다. 실제로 매우 많은 변수들이 존재할 수 있기 때문에 앞서 계산한 방식으로 바로 극값을 찾아내지 못할 가능성이 매우 높다. 따라서 다양한 상황에서 사용할 수 있는 계산방식이 필요한데, 그 중에서 가장 대표적인 최적화 방식으로는 경사하강법이 있다.

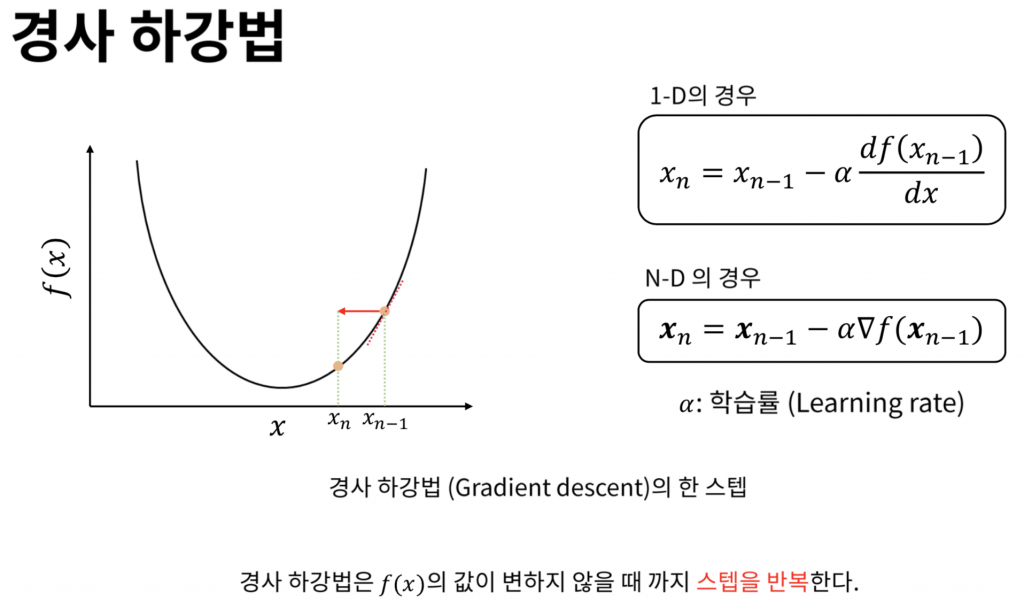
이렇게 $\alpha$ 라는 스텝 길이를 설정하여, 각 기울기에 맞게 점점 가장 낮은 부분으로 내려갈 수 있다. (경사하강법은 하나의 최적화 방식으로, 항상 기울기에 비례한 스텝을 내려가는 것은 아니다.) 이렇게 가장 낮은 골짜기를 찾게 되면, 최적의 변수를 찾아낼 수 있다.

하지만 경사하강법에도 여러 문제점이 존재한다.
$\alpha$ 의 값이 너무 작거나 크게 되면, 다음과 같은 일이 발생하게 된다.

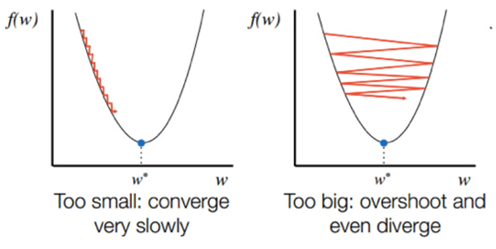
너무 작다면 시간 내에 최적화가 되지 않거나, 너무 크다면 아예 위로 발산해 버리는 경우가 나타날 수 있다. 또, 아래의 그림과 같이 하나의 극솟값을 가지지 않는 경우, local minimum 에 수렴하는 경우 또한 존재한다.

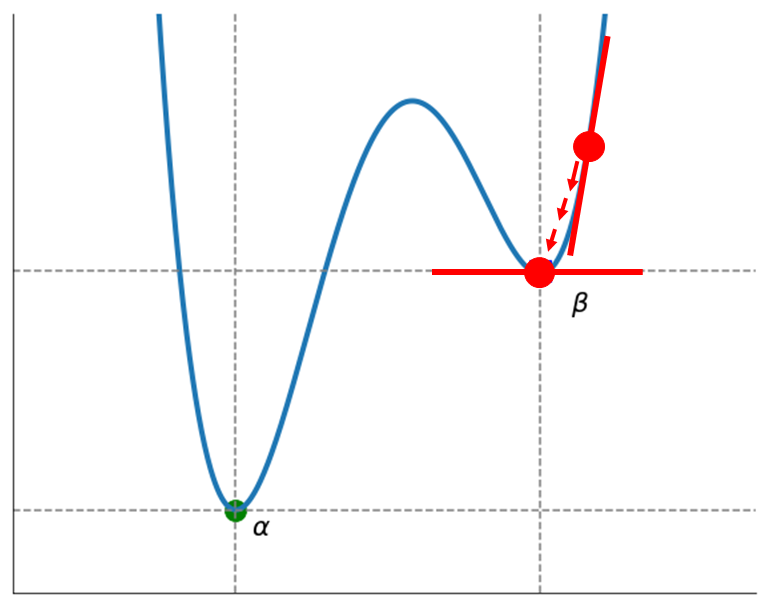
따라서 스텝의 길이를 적절히 설정하고, local minumum 에 도달하지 않게끔 설정해주는 것이 경사하강법의 중요한 요소가 될 것이다.

3. Logistic regression

Linear regression에 대해서 알아보았는데, 그렇다면 우리는 왜 Logistic regression 을 사용해야 할까?? 아래 예시를 살펴보자.

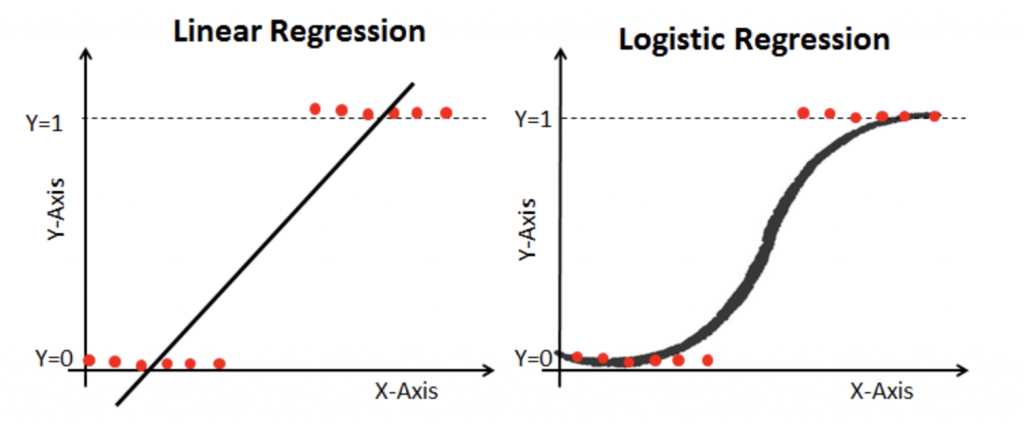
$x$가 0 ~ 50 일때는 $y$ 가 0이고, $x$가 50 ~ 100 일때는 $y$가 1의 값을 가진다고 생각했을 때, 앞서 배운 linear regression 으로 그래프를 그리게 되면, 무언가 찜찜한 그래프가 나온다. 맞는 것 같으면서도 아니고,, 아닌 것 같으면서도 맞고…

이런 경우를 제대로 회귀분석을 하기 위하여 Logistic regression 을 사용하는데, 이 그래프의 정체부터 밝혀보자면 다음과 같은 식을 가진다.

$$P = \frac{e^{a+bx}}{1 + e^{a+bx}}$$

흔히 sigmoid 라는 곡선이라고 불리는데, 왜 이런 그래프 모양이 나오는지 알기 위해서는 Odds Ratio 개념을 이해해야 한다.

앞서 말했던 예시를 다시 살펴보았을 때, $y$가 1이 될 확률과 0이 될 확률을 비교하여 나타내는 수치로, 다음과 같이 나타낼 수 있다.

$$ Odds\;Ratio = \frac{y = 1일 확률}{y = 0일 확률} = \frac{P}{1-P}$$

그리고 이 값이 $log$를 씌운 값이 (Logit, 로짓이라고 불린다) Logistic regression 에서의 $y$로 들어가게 되어 다음과 같이 식이 변환되게 된다. (Sigmoid 함수와 선형 회귀가 결합된 형태로 생각할 수 있다.)

$$\begin{align} &\ln{(\frac{P}{1-P})} = a + bx \rightarrow \frac{P}{1-P} = e^{a + bx} \\ &P = e^{a + bx}(1-P) \rightarrow (1 + e^{a + bx}) P = e^{a + bx} \rightarrow P = \frac{e^{a+bx}}{1 + e^{a+bx}} \end{align}$$

따라서 아까 이야기했던 Odds Ratio 를 통해서 x값에 따른 P를 계산해내게 되면, 어떤 부분에 속하는지를 구별할 수 있다. ($P > 1$이면 사건 발생, $P < 1$이면 사건 발생 안함)

마찬가지로 Loss가 최소가 되는 계산법을 적용하여 변수를 선택해야 하는데, 2차원 그래프 (변수 1개) 에서는 마찬가지로 최소제곱법을 이용하기도 한다고 한다. 만약 변수가 2개 이상이 되어 차원이 더욱 늘어나게 되면, Sigmoid 함수 말고 Softmax 함수 (활성함수) 등을 사용하기도 하고, 변수 선택에도 여러 방식들이 적용되어 경사하강법 등 여러 방식들을 채택하기도 한다.

물론 지금은 다루지 않을 내용이지만,

1. Feedforward Selection
2. Backward Elimination
3. Stepwise

등이 있다고 한다. 추후에는 활성함수가 무엇인지도 다룰 계획이니, 이번 포스트에서는 회귀분석의 종류와 개념에 대해서 알아보고, 다음에 제대로 어떻게 쓰이는지를 다루어보도록 하자.

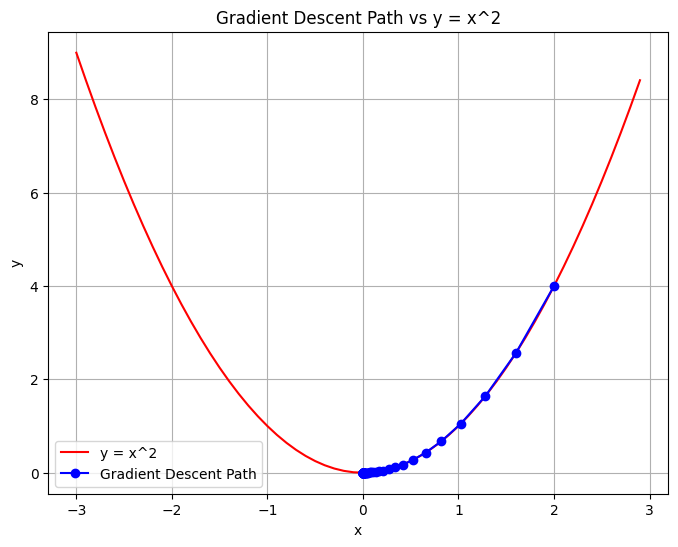
∞. Exersize

import torch
import matplotlib.pyplot as plt

x = torch.tensor([2.0], requires_grad=True) # (2, 4)

learning_rate = 0.1
num_iterations = 100

x_values = [x.item()]
y_values = [x.item()**2]

for i in range(num_iterations):
    y = x**2
    loss = y
    loss.backward()
    
    x.data -= learning_rate * x.grad
    x.grad = None
    
    x_values.append(x.item())
    y_values.append(x.item()**2)

# Original y = x^2 graph
x_range = torch.arange(-3, 3, 0.1)
y_range = x_range**2

# plotting
plt.figure(figsize=(8, 6))
plt.plot(x_range.numpy(), y_range.numpy(), label='y = x^2', linestyle='-', color='r')
plt.plot(x_values, y_values, marker='o', linestyle='-', color='b', label='Gradient Descent Path')
plt.title('Gradient Descent Path vs y = x^2')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()